Теорема Чебышева - Постулат Бертрана.

Для любого натурального n>1 найдется простое число p, такое, что n<p<2n.

Доказательство.

Для доказательства используем следующие обозначения:
[x] - целая часть числа x (наибольшее целое число, не превосходящее x).
- С_a^b - число сочетаний из a по b (оно равно a!/(b!*(a-b)!)).
Пусть - множество всех простых чисел.
Пусть q(x)=.
1) Докажем, что q(n)<n*ln(4) при всех натуральных n. Докажем данный факт по индукции.
Для n=1 q(n)=0<1*ln(4). Для n=2 q(n)=ln(2)<2*ln(4). База индукции доказана. Докажем и переход индукции.
Если n>2 и n четно, то n не является простым числом, т.е. q(n)=q(n-1)<(n-1)*ln(4)<n*ln(4).
Если n>2 и n нечетно, то пусть n=2m+1 (m>0). Тогда получаем

.
Любое простое pÎ(m+1; 2m+1) делит числитель данной дроби, но не делит ее знаменатель. Отсюда дробь делится на все такие простые числа, т.е. не меньше их произведения:
. Взяв логарифм от обеих частей, получаем: q(2m+1)-q(m+1)ln(4^m)=m*ln(4). Т.к. q(m+1)<(m+1)*ln(4), то и
q(2m+1)<m*ln(4)+(m+1)*ln(4)=(2m+1)*ln(4)=n*ln(4). Переход индукции доказан.

2). Докажем теперь саму теорему-постулат. Будем доказывать от противного: пусть существует такое натуральное n>1, что нет ни одного простого числа на интервале (n; 2n). Если 2n2048, то одно из простых чисел 3, 5, 7, 13, 23, 43, 83, 163, 317, 631, 1259 и 2503 (каждое меньше удвоенного предыдущего), назовём его p, удовлетворяет неравенству n < p < 2n. Следовательно, n≥2048.
Теперь будем оценивать число . . Т.к. - максимальный член этой суммы, то отсюда следует, что . Пусть R(p,n) - степень p в разложении на простые множители. Т.к. n! имеет для каждого j имеет ровно 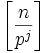сомножителей, делящихся на p^j, то в разложении n! на простые множители p входит в степени . Ввиду того, что =(2n!)/(n!)², то . Заметим, что каждое слагаемое вида равно либо 0, либо 1 (равно 0, если дробная часть меньше 1/2 и равно 1, если эта дробная часть не меньше 1/2). Заметим, что все слагаемые, начиная с в этой сумме равны 0. Т.к. R(p,n) - сумма слагаемых, каждое из которых равно 0 или 1, то . Оценим теперь p^R(p,n): . Эта оценка верна для любых p. Более лучшую оценку можно получить для . Для таких p количество слагаемых равно 1, т.е. .
А теперь посмотрим, в каком интервале находятся делители числа . Оно не имеет таких простых делителей p, что
а). 2n<p, т.к. ;
б). n<p<2n, т.к. мы предположили, что в этом интервале нет простых чисел.
в). 2n/3<pn, то (т.к. n5 из p>2n/3 следует, что ), что дает нам .
Отсюда у нет простых делителей, больших 2n/3. Теперь оценим произведение p^R(p,n) по всем простым делителям p числа : для чисел p произведение не превышает . А для делителей, больших оно не превышает . Ввиду того, что равен произведению p^R(p,n) по всем простым p, то мы получаем следующее двойное неравенство:. Используем утверждение части (1) доказательства, что q(n)<n*ln(4). Отсюда мы получаем:. Далее сокращаем обе части неравенства на 4^2n/3 и используем то, что 2n+1<(2n)² (n>1). После этого получается . Далее замечаем, что (n18), т.е. . Прологарифмируем обе части:
ln(4)*n/34/3**ln(2n), т.е. 2*ln(2)*n4**ln(2n). Делим обе части на >0: .
Далее делаем подстановку 2^2t=2n. Тогда =2^t; ln(2)/ln(2n)=1/(2t), поэтому , что верно лишь при t<6. Но тогда 2n<2¹²=4096, т.е. n<2048. Противоречие, т.к. у нас n2048. Отсюда при любом натуральном n>1 найдется простое p такое, что n<p<2n.

Немного истории: Постулат Бертрана (теорема Бертрана-Чебышёва, теорема Чебышёва) гласит, что для любого n ≥ 2 найдётся простое число p в интервале n < p < 2n. Такая гипотеза была выдвинута в 1845 году французским математиком Джозефом Бертраном (проверившим её до n=3000000) и доказана в 1850 Пафнутием Чебышевым. Рамануджан в 1920 году нашёл более простое доказательство, а Эрдеш в 1932 - ещё более простое. Здесь было приведено доказательство Эрдеша.